Relative importance

---

Relative importance

Here, we calculate the expected relative importance of our effect of interest only (for more information, see Indlekofer and Brandes, 2013). We present only a perspective of RI (a) aggregated over all actors and (b) at time-point 1.

The following scripts reproduces the pie charts presented in the manuscript (Figure 7):

# We use a function to load the objects under new names.
loadRData <- function(fileName){
  #loads an RData file, and returns it
  load(fileName)
  get(ls()[ls() != "fileName"])
}

# get the RSiena object lists for both models (frequency and volume)
mydata_freq <- loadRData("clubdata_rsiena_freq.RData")
mydata_vol <- loadRData("clubdata_rsiena_vol.RData")

# we calculate RI of effects pertaining to running activity dynamics (both frequency and volume) across clubs


# we make a list, in which we store RI-objects for each club
RI_list <- list()

for (i in 1:5) { # for each club

  #get sienaFit list 
 
  ansL <- loadRData(paste0("test/sienaFit/sienaFit_club", i, ".RData"))

  #take model 5 (avAttH, avAttL, indegree...)
  ans <- ansL[[5]]
  
  # get only parameters for the evaluation function
  theta.eval <- ans$theta[ans$effects$type[ans$effects$include]=="eval"]
  myeff.eval <- ans$effects[ans$effects$type[ans$effects$include]=="eval",]
  
  # only effects we are interested in
  myeff.eval.beh <- myeff.eval[c(1, 16:20), ] 
  # note: also include outdegree (or another effect pertaining to network dynamics); apparently this is needed...
  # first, I excluded the shape effects, as they heavily compound the resulting plots (they are most important...)
  theta.eval.beh <- theta.eval[c(1, 16:20)] 
  
  # algorithm used
  myalgo <- sienaAlgorithmCreate(projname = "test", nsub=5, n3=5000 )
  
  # use sienaRI()
  RI <- sienaRI(
    data = mydata_freq[[i]],
    theta = theta.eval.beh,
    algorithm = myalgo,
    effects = myeff.eval.beh
  )
  
  # extract RI for the behavior dynamics
  RI_beh <- RI[[2]]
  
  # take the statistics for time t
  t = 1
  RI_freq <- RI_beh$expectedRI[[t]]
  
  # and repeat the same procedure for volume
  ansL <- loadRData(paste0("test/sienaFit/volume/sienaFit_club", i, ".RData"))
  ans <- ansL[[5]]
  theta.eval <- ans$theta[ans$effects$type[ans$effects$include]=="eval"]
  myeff.eval <- ans$effects[ans$effects$type[ans$effects$include]=="eval",]
  myeff.eval.beh <- myeff.eval[c(1, 16:20), ]
  theta.eval.beh <- theta.eval[c(1, 16:20)]
  RI <- sienaRI(
    data = mydata_vol[[i]],
    theta = theta.eval.beh,
    algorithm = myalgo,
    effects = myeff.eval.beh
  )
  RI_beh <- RI[[2]]
  RI_vol <- RI_beh$expectedRI[[t]]
  
  # combine 
  RIc <- c(RI_freq, RI_vol)
  
  # put in the list
  RI_list[[i]] <- RIc
}

# we make a dataframe for plotting multiple pie charts
df_plot <- data.frame(
  ri = unlist(RI_list),
  eff = substring(RI[[2]]$effectNames, 15),
  y = rep(c("Frequency", "Volume"), 10, each=5),
  club = rep(c("Club 1", "Club 2", "Club 3", "Club 4", "Club 5"), 1, each = 10)

)

# alter effect names
df_plot$eff <- as.factor(df_plot$eff)
levels(df_plot$eff)[1] <- substring(levels(df_plot$eff)[1], 14)
levels(df_plot$eff)[2] <- "other activities"

# reorder effect for plot
df_plot$eff <- factor(df_plot$eff,
                     levels = c("indegree", "average attraction higher", "average attraction lower", "gender", "other activities"))
# nice colors
color <- brewer.pal(5, "Set2")

ggplot(df_plot, aes(x="", y=ri, fill=eff)) +
  geom_bar(width = 1, size = 1, color = "white", stat = "identity") +
  coord_polar("y") +
  geom_text(aes(label = paste0(round(100*ri), "%")), 
            position = position_stack(vjust = 0.5)) +
  labs(x = NULL, y = NULL, fill = "Effects", 
       title = "<b><span style = 'font-size:16pt'>Relative Importance (<i>RI</i>) of indegree and attraction higher/lower effects</span>",
       caption = "<span style = 'font-size:10pt'><i>Note</i>: percentages indicate the extent to which effects determine whether actors make changes in their running attributes (i.e., frequency and volume).
       Percentages indicate the importance of model parameters relative to one another. They should not be interpreted as absolute explained variance. Patterns presented here would change, would we include other effects (e.g., basic shape effects, covariate effects). 
       The pattern of relative importances of effects was consistent across time; here, we present t=1.") +
  guides(fill = guide_legend()) +
  scale_fill_manual(values = color) +
  facet_grid(y~club, switch = "y") +
  theme_classic() +
    theme(axis.line = element_blank(),
      axis.text = element_blank(),
      axis.ticks = element_blank(),
      legend.title = element_blank(),
      
      plot.title = element_textbox_simple(
        padding = margin(5.5, 5.5, 5.5, 5.5),
        margin = margin(0, 0, 5.5, 0),
        fill = "lightsteelblue2",
        lineheight=1),
      
      strip.text.x = element_textbox(
        size = 9,
        color = "white", fill = "#5D729D", box.color = "#4A618C",
        halign = 0.5, linetype = 1, r = unit(5, "pt"), width = unit(1, "npc"),
        padding = margin(2, 0, 1, 0), margin = margin(3, 3, 3, 3)
      ),
      
      strip.text.y = element_textbox_simple(
        size=12,
        face="bold.italic",
        vjust=1),
      
      strip.background = element_blank(),
      
      plot.caption = element_textbox_simple(
        padding = margin(2, 2, 2, 2),
        margin = margin(0, 0, 2, 0),
        fill = "lightsteelblue2",
        lineheight=1,
        vjust=1.5,
        r = grid::unit(8, "pt")))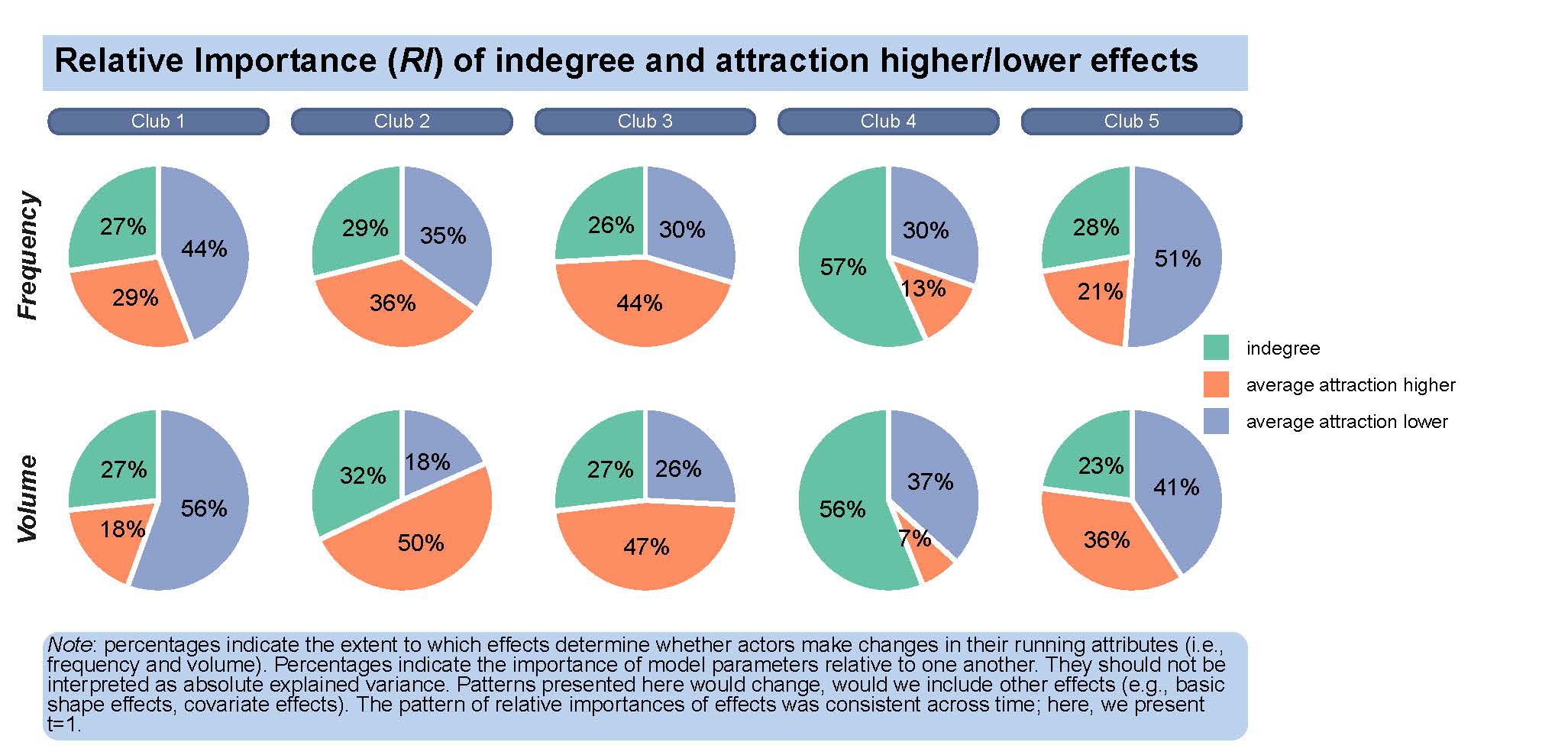

---

References

Indlekofer, Natalie, and Ulrik Brandes. 2013. “Relative Importance of Effects in Stochastic Actor-Oriented Models.” Network Science 1 (3): 278–304. doi:10.1017/nws.2013.21.

---

Copyright © 2021 Rob Franken